“Who of us would not be glad to lift the veil behind which the future lies hidden; to cast a glance at the next advances of our science and at the secrets of its development during future centuries? History teaches the continuity of the development of science. We know that every age has its own problems, which the following age either solves or casts aside as profitless and replaces by new ones. If we would obtain an idea of the probable development of mathematical knowledge in the immediate future, we must let the unsettled questions pass before our minds and look over the problems which the science of today sets and whose solution we expect from the future.” (David Hilbert, The 23 Problems)

Warianty fasady budynku Muzeum Sztuki w Bejrucie, (c) HW Architecture
Whoever speaks of contingency and risk must have in mind the notion of chance. When things happen by chance, they just follow no law. Chance was tamed after the discovery of statistical regularities.1 Scientists and metaphysicians started talking about the laws of chance. By that, they meant probabilistic laws. Probability thus emerged.2 Even the laws of physics were found to be indeterministic at bottom.3
Randomness is linked to statistics and probability. We imagine random processes, that is to say, repetitions of a random draw. Who speaks of repetition presupposes a fixed framework, or chance setup, in which the draw takes place and which can be trialled repeatedly. Behind chance, the fixity. The outcomes are different but the set of conditions is the same. We would hardly call random a one-time chance occurrence. It is better to call it an event.
The philosophy of the event is different from the philosophy of probability. The future is truly unknown. There is no predetermined list of possible scenarios. Even if all the future outcomes that the world is ever going to draw from the urn are elements of “sample space” – as abstract probability theory requires – the scenarios, or the accounts of what might happen, or again, the conceivable events, are not present beforehand. They become thinkable and narratable after the unmeasurable occurrence. The “algebra of events” undergoes a massive recalibration.
It thus becomes a purely metaphysical decision to suppose that the samples were already all there underneath the events or, alternatively, that the events truly emerged from the void and there was no urn to draw from. This makes no difference for physical objects whose fate is localized and cannot be otherworldly. Probability theory was designed for them, eventually to end up with Markov processes in which the state of the object is recognized as the fundamental variable and becomes confused, by extrapolation, with the state of the world. This is a metaphor that is only made to fit the size of the physical object, and no real extrapolation to the world at large should be attempted.
Probability theory was not designed for metaphysical objects like the world or the market. Contingency is better suited than possibility in this respect. To say that a thing is contingent is to say that it could be different from what it is, without specifying its state, or what different possible things it could be. It could be absolutely different. As a matter of fact, it could be different from what it is in the sense of not being at all – a hardly tenable condition for the notion of a possible state.
1. Universe and World
It is fascinating that Hilbert should speak of unveiling the future in relation to mathematics. He speaks of the “continuity” of history and exercises speculation. He tries to predict the future of mathematics constructively by identifying its present problems and offering guidelines for their future resolution. It is then interesting to realize that the history of the problems turned out to be radically different, discontinuous to say the least, and unconceivable by Hilbert himself. Gödel's incompleteness theorem was the perfect earthquake relative to Hilbert’s construction program. Precisely, Hilbert had used the word “probable” in relation to the future history of mathematics, when the word “event” or “paradigm shift” would have been more appropriate. As a matter of fact, the sixth problem on Hilbert’s list of 23 problems was precisely to try to found probability on axiomatic theory.
Hilbert presented his 23 problems at the opening of the International Congress of Mathematicians in Paris, in 1900. The background was the universal exhibition of 1900 and the main new Parisian attraction was the Eiffel Tower, which was erected for the opening of the previous universal exhibition, in 1889. Not only was Hilbert speculative in terms of unveiling the future of mathematics through the list of 23 problems, but he was doubly speculative. Indeed, the second problem on the list was the first step of a program to solve any future mathematical problem: to construct a universal algorithm that would assess the truth or falsity of any mathematical statement. Even worse than universal, Hilbert’s speculation was the end of the world of mathematics, we may say; it aimed to bring every mathematical problem to a stop.
Probability theory speaks of the universe, or sample space. Markus Gabriel distinguishes between universe and world.4 The universe is the collection of physical objects and is described by the physical laws that they follow. The world is a much larger entity. There is the physical world but there is also the world of dreams, the world of art, the world of lovers, the world of books, etc., and the world of man. We usually speak of the end of the world rather than the end of the universe and Heidegger coins the term “being-in-the-world”. Gabriel even argues that the world cannot exist because the totality of imaginable things cannot exist. Using the term “world” is usually the indication of a metaphysical rather than a physical discourse.
Note that the exhibitions leading, in 1889 and 1900, respectively to erecting the Eiffel Tower and to presenting Hilbert’s 23 problems are called universal and that the Louvre is considered a universal museum. Before it was decided that the Louvre will provide the name and the content, the program handed over to the architect in Abu-Dhabi was to design a “universal museum.” A museum is universal when it is trans-historical and trans-geographical; it collects and exhibits artefacts produced by man in all places of the inhabited world and in all periods of lived history. So it is the terminus of all collections, an end of the world, of sorts.
When the agreement was signed between France and the Emirate of Abu-Dhabi and the announcement was made that this new universal museum would be the Louvre, the news came as a surprise to many, even as a shock. The name of the Louvre would now emerge in the desert and the expression “Louvre of the Desert” was coined. To the end of the world, to the end of all times and all collections, we had now added a major earthquake. Also, the Louvre was now doubly universal, not only aiming to cover all places and all times but no longer itself being attached to a particular place or even particular time. It could be located both in Paris and Abu-Dhabi, both in our future and our past. It became the universal-universal museum, extending and remaining forever. In a way, it too was meant to resolve all future problems. A true challenge to the architect, and speculation all over again.

Louvre Abu-Dhabi, © TDIC, Architekt: Ateliers Jean Nouvel.

Louvre Abu-Dhabi, © TDIC, Architekt: Ateliers Jean Nouvel
2. Speculation
1900 is the year Bachelier published his Theory of Speculation. In it he described the mechanics of the stock exchange, especially the transactions “with a premium” which are known as “options” today, or more generally, “derivatives.” In the process, he even gave the first (heuristic) mathematical treatment of Brownian motion. The option pricing formula is almost identical, in Bachelier, to the one that Black and Scholes will discover in 1973.
Hilbert’s sixth problem began in 1900 and ended in 1933, when Kolmogorov published his monograph and finally established probability on the basis of axiomatic theory. Bachelier’s speculation was also speculation in the sense that Brownian motion, which he did not recognize by this name, wasn’t even warranted to exist. Wiener proved it existed by constructing it, in 1920, using a result by Daniell on stochastic processes, which was a precursor of Kolmogorov’s. The usual order of presentation, in modern texts, is to construct Brownian motion after Kolmogorov’s extension theorem, that is to say, after the axiomatic theory he had laid down.
The market crashed in 1929 and option trading was banned, as buying the put options that were described by Bachelier was identified with gambling against the prosperity of the nation. Put options returned in favor in 1973 after Black and Scholes showed an exact option pricing formula by replication of the option payoff. The option (call or put), or generally, the derivative, was no longer perceived as a gamble on the price of the underlying asset but became an extension of it and of its trading. As a matter of fact, Black, Scholes and Merton showed that derivatives were redundant with the underlying asset they were written on. Options could now be manufactured safely; their trading became an industry and was no longer a game, and market-makers of options crowded the trading floors after 1973.
The market crashed again in 1987 because traders, as a consequence of the BSM algorithm, had precisely left it to programs to synthesize the options and to do the trading in their place, when options were not in fact redundant. As a matter of fact, the October 1987 crash was the real birth of the options market, in the sense that it imposed their independent trading (volatility smile). In the end, options are neither gambles nor redundant structures. Both probabilistic pictures that try to frame them are wrong. Options are not supplemental, superfluous, parasitical, or in a word, dangerous and pernicious. They are independent assets. To be independent is not to be dangerous. In order to emphasize the independence and therefore the virtue of derivatives, I prefer to call them “contingent claims”.
3. Beirut
In 1929, Charles Corm built his emblematic skyscraper, which he had designed himself and was for a while the tallest building in Beirut. He drew his inspiration from the Chrysler Building in New York. Corm’s building was home to the company he had founded after obtaining a license from Henry Ford (who he had met in New York in the early 1920s) to represent the Ford company in the Middle East. The building was known as The Ford Motor Company’s Middle East Headquarters, later to be named The Corm Building and Gardens. The plan was to assemble the Ford Model T locally and distribute it in the region.
The Ford Model T was born in 1908, one year before Emile Borel showed a much unexpected result in probability, known as the strong law of large numbers. It is said that its largescale distribution by Corm in the Middle East, through the various branches of the business he had implanted, was one of the reasons roads were created in the region, leading even to the formation of the oil states. The piece of land that Corm owned in Beirut was located right at the start of the Damascus Road, however he built his tower a little bit in retreat for fear that it might collapse, in the event of an earthquake, and cut the road which was so vital for the Middle East.
For a while, the Eiffel Tower was the highest building in the world, until the Chrysler building was erected in New York. Beirut was home to one of the best Roman law schools of antiquity. Law and courts of justice are the original place of probability: when it is argued from evidence that the defendant is “probably”, that is to say, provably, guilty. In the modern history of probability, we distinguish between the French school (Borel, Lebesgue, Fréchet, Lévy) and the Russian school (Markov, Kolmogorov, Chebyshev). It is said that Beirut was destroyed and rebuilt seven times in its 5000-year history.
Nassim Taleb, option trader in the formative days of the 1987 crash, author of The Black Swan and the first critic of probability in relation to the derivatives markets, was born in Amioun, a village not far from Beirut. Today’s number one derivative software company (historically the first to have booked each option under a different volatility number, in accordance with the emergence of the volatility smile and in disagreement with the whole probability paradigm underlying BSM) was also founded in the wake of the 1987 market crash by two brothers who were born in Beirut.
The elder brother, an engineer with chemistry as a hobby, grew to become one of the largest collectors of minerals and crystals in the world. He later donated his collection to a museum that he created and opened in Beirut, in 2013, across the garden of the Corm building, even closer to the Damascus Road.
The younger brother was my boss when I started a career as an options trader. My first day on the trading floor was the day the market crashed, 19 October 1987. I was born in Beirut too and the two books I wrote to try to explain the volatility smile and how it disrupts the schema of probability have as subtitles, respectively, The End of Probability and An Inverse View of the Market.5
4. Probability
To formalize probability and solve Hilbert’s sixth problem, Kolmogorov introduced the notion of sample space. This is the big urn, also known as the universe, from which the world draws the random outcomes, or cases, symbolized by ω. The case, or that which happens concretely, the contingent “this” (as in the expression “this is what happened”), is unmeasurable and indescribable. It may even be unconceivable, that is to say, conceivable only by God. Random phenomena are by definition connected to the concrete world; the concrete world cannot but be part of the picture of randomness; thus, there must be, underneath the event and triggering it, the notion of the concrete sample.
When we throw the dice, we are only interested in the events described by the numbers on the face, because we adopt the point of view of playing the game of dice. The game, or the reality we are now contemplating, is a screen, an abstraction of the concrete world. We separate the concrete and the abstract and we distinguish between the absolutely concrete situation and thinkable reality. Indeed, what the sample is, in its absolute concreteness, or what the world has accomplished at bottom in order to produce the trial, doesn’t stop at the number shown on the face. It extends into the unthinkable abyss of the whole concrete situation.
I did say “whole.” This means that describing the whole situation involves the question of whether it was sunny or rainy when the die was cast, and whether the player was smiling or frowning, and whether his arm was strong enough to lift the die and throw it, and whether gravity on Earth was permanent enough to attract the die on the ground, etc.
Abysmal as it may be, the concrete world as represented by the formalism of probability is not compatible with the radical event. Because there is virtually no end to the description of the situation in its absolute concreteness, because the concrete situation triggering the event “six” when the die is cast could be further refined by saying that the die was red and the player was smiling and the sun was shining and gravity was on earth, to which we might add that the die had as a matter of fact landed a “four” the second time it was thrown, and a “two” the third time, etc., or that it was raining at the hundredth throw, and that a meteorite had fallen and killed the player at the millionth, etc., because everything that will have ever happened in the history of the universe could be virtually recounted as a single sample that the world has drawn, once and for all, from the origin until the end of times, a cut is established at some level of the abyss, a point of view is distinguished, a physical object is carved out of the world, and this automatically entails that the object has multiple faces and that multiple samples can produce the same face – samples now distinguished solely by something the point of view can no longer distinguish. This brings about repetition, and therefore randomness in the ordinary sense. Now that we have suspended the fall and broken the “once and for ever,” we can only repeat.
In truth, we should never regress in thought towards an ever-totalizing sample space. Probability should not be extrapolated beyond its modest project. It was only meant to deal with a universe of things, totalized once and for all, not with the world. But perhaps a new metaphysics of chance should be sought beyond probability and the whole logic of abstraction questioned. What alternative logic? One in which the abyss is no longer the passive and regressive cause of randomness but is spontaneously thrown forward.
5. Trading
Money is invented. It becomes the only end of the world. You can only make money or lose money. The stock price can only go up or go down. As soon as a stock exchange is given, randomness is given. The infrastructure of sample space is no longer needed. Speculation, or the market looking at itself reflexively, becomes the only ground, a constantly shifting ground.
Probability is the result of abstraction, whereas money and price are concrete. It is only regressively that the events of probability theory (that is to say, thinkable reality) made contact with the absolute concrete. As we said, the abyss kept being dug out beneath the surface, in a desperate move always to reconstruct the future as already present in the past, as already an element of the total. But the future shouldn’t be part of the absolute concrete, at least not in a logic where every difference is rewritten in the past! It shouldn’t be a refinement of what the draw, once and for all, is keeping for us! The future should be absolutely different, absolutely contingent. It should be different, only we don’t know different from what.
And how could the abyss be thrown forward? How could the concrete world, which is now screened off by money, recover its absolute richness and infinite detail? How could the future be concrete yet remain absolutely open? By pushing money and trading to their ultimate consequence, which is the market of contingent claims.
Trading is not a matter of drawing a sample from an urn. Trading means randomness. Accordingly, when the stochastic processes that we write in finance, typically Brownian motion, are no longer seen as the result of abstraction of the abysmal concrete but of the conceptualization of the trading pit, when there is no longer a sample space to draw from repeatedly but only price to follow its single fate (going up or going down) and only money to show its single face (being made or being lost), BSM shows that this new view of randomness, no longer extensive but intensive, no longer as a succession of draws but as a single trading strategy, is equivalent to the replication of contingent payoffs, and consequently, to the writing of contingent claims. Now these, once written, can only be traded in their turn, because the sample space is suppressed and the only remaining pit is the trading pit.
Trading a stock is the same as writing a derivative on that stock, is the same as trading the derivative, is the same as writing a derivative on the derivative, is the same as trading the second derivative in turn, etc. In a single stroke, the infinity of the concrete world is handed back from the other end, never to be totalized again in a universe of cases. The abyss opens forward, spontaneously. Kolmogorov dies on 20 October 1987.
6. The Desert
Designing a universal museum in the desert is not a matter of redistributing probability or substituting a case for another in a fixed universe of cases, or even a matter of changing the point of view over a fixed sample space. It is repetition in the metaphysical sense; it is architecture experiencing the end of its world and not just testing the limit of its universe. The Louvre is not swallowed by an actual earthquake but by a conceptual one. The earth that shakes, in this case, is not one that urges the architect to build a replica of the original model, or a modern reinterpretation, but lies at a deeper level.
Cities, and not just single buildings, are wiped out by earthquakes, so they ought to come first in the aesthetics of contingency, where being alternates with non-being, and fulguration with annihilation. Cities, with their circulation and communication networks, with their whole language, come before the single building when the whole ground shifts, and for this reason Jean Nouvel confronts his conceptual/contextual earthquake by making the museum emerge in the desert as a whole city. The earthquake becomes part of his architecture and is no longer a preliminary phase. The moment the city is levelled no longer alternates with the moment it is rebuilt; they become the same moment. In this lies the singularity of the Louvre of the desert and it is only logical that it should be marked by a phenomenal sign – in this case, the prodigious dome covering the city.
The architect didn’t find the parts with which to rebuild it after the conceptual earthquake in the subsoil of Paris, but in a deeper layer – even a deeper concept – of the earth. The earth didn’t deliver parts of Paris, this time, but all of Paris, or perhaps an anamorphosis of it. Architecture found a new variable underlying its function, no longer building on a place on earth, but building through the earth. All of architecture was displaced. The metallic dome of the Louvre of the desert has exactly the same weight as the Eiffel Tower. It is the Eiffel Tower, we might say, only processed by the earth: the new universal exhibition of Paris over the new universal museum.
Through the perforated dome, the architect pours light over the city. He transforms what’s most abundant and overwhelming in the desert, the sun, into what’s scarcest and most precious, the rain, thus creating a rain of light. It is not clear whether the gigantic sieve emerged from the sand, from the sea, or came from the sky. It is only logical that the elements should be confused when architecture tests its limits and the origin of light and geometry is probed. The compression is such, in the singularity, that the dome may as well be a complex crystal forged by the abysmal labor of the earth.
7. The Earth
Hala Wardé, Nouvel’s partner who executed the Louvre project, was born in Beirut. Her family came from Damascus. If Nouvel can claim the concept and the form, Wardé can claim the earth that gave birth to the material construct. Every detail that was designed, every structure that was assembled, every procedure that was followed, was the result of her work and her team’s. Given the earth-moving event of the Louvre of the desert, you can then either try to conceive its incredible realization, an impossible task, or stop at the idea that the whole material script lies in Wardé’s archives. In the way it put an end to Hilbert’s universal program, Gödel’s numbering procedure did nothing different.
It is fascinating to see how Nouvel responded to the universality of the problem presented to him (a double universality, we said); how he created a city, a geometry, a sky and almost light, almost out of nothing, out of the desert, out of the very limit of his universe and its codes. It is then interesting to see how Wardé, who was the earth to Nouvel’s earthquake and fulguration, will herself move after all this and what building she will now personally design.
The abyss is thrown in the opposite direction, and the city, of course, is Beirut. The city of light may have re-emerged in the desert under a new form, but Wardé’s problem, who won the competition to design the Beirut Museum of Art (BeMA), is harder. How to make Beirut emerge, the city of the end of probability and of the seven earthquakes? How to build, not over the abyss, but through the abyss? How to build the abyss itself?

Muzeum Sztuki w Bejrucie: plan i przekrój. (c) HW Architecture
The earth was already at work in transporting the Louvre from Paris to the desert, in acting beyond the limit of the universe and even beyond the end of the world. So now we wonder how Wardé, who was the earth of this earth, could take the earth’s work a step further. It is not a case of rebuilding a destroyed city, or making an inexistent city emerge, but something deeper. What could be next, indeed, if not inverting the world?
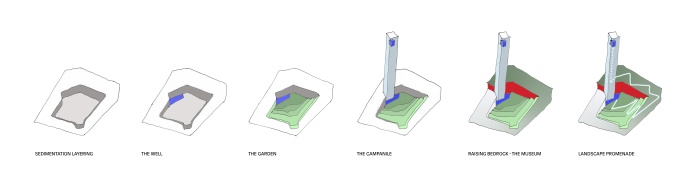
Muzeum Sztuki w Bejrucie. Kolejność prac. (c) HW Architecture
The site is exactly located at the start of the Damascus Road, adjacent to the Corm’s building and to the museum of crystals and minerals. The origin of the name of Beirut, Bîr, signifies a well. By digging the foundation of her building, Wardé in fact drilled a well. The water, flowing to the surface of the earth, could not but produce a garden, and the earth, moving to one side, created an acclivity, under which the actual museum is lodged.
The abyss, however, would not be content unless the world could rise to counterpoise it. This, Wardé achieved with the campanile, a slender tower of virtually infinite height and infinite charge. In probability, this is known as the Dirac distribution. In reality, this is an intensive sign, known as Aleph.
BIO
Elie Ayache was born in Lebanon in 1966. He was trained as an engineer at l’École Polytechnique of Paris and he pursued a career of option market-maker on the floor of MATIF (1987–1990) and LIFFE (1990–1995). He then turned to the philosophy of probability by earning a DEA at la Sorbonne. In 1999, he co-founded ITO 33, a financial software company, specialized in derivative pricing technology. Today, ITO 33 is the leading specialist in the pricing of convertible bonds, in the equity-to-credit problem, and more generally in the calibration and recalibration of volatility surfaces. Ayache has published numerous articles on the philosophy of contingent claims. He is the author of The Blank Swan: The End of Probability (2010), and of The Medium of Contingency: An Inverse View of the Market (2015).
* Cover photo: Beirut Museum of Art Façade Variations, (c) HW Architecture
[1] Ian Hacking, The Taming of Chance (Cambridge: Cambridge University Press, 1990).
[2] Ian Hacking, The Emergence of Probability (Cambridge: Cambridge University Press, 1975).
[3] Lawrence Sklar, Physics and Chance (Cambridge: Cambridge University Press, 1993).
[4] Markus Gabriel, Why the World Doesn’t Exist (Cambridge and Walden: Polity Press, 2015).
[5] Elie Ayache, The Blank Swan: The End of Probability (Chichester: John Wiley & Sons, 2010) and Elie Ayache, The Medium of Contingency: An Inverse View of the Market (Basingstoke and New York: Palgrave Macmillan, 2015).