Each of us has those. It is not the eyes, the nose the lips that make a person beautiful,
but the spaces between them, that is the proportions.
(Janusz Kapusta, Plus Minus, Podręcznik do myślenia, Zysk i S-ka, 2014)
In this essay I wish to focus on the amazing discovery which I made in New York around 2000 thanks to which beauty became – at least for me – not only inevitable but also palpable.
I have discovered the unknown rules of the golden ratio. In 2003, as the only non-mathematician I was invited by the professor of mathematics at Jay Kappraff’s New Jersey Institute of Technology and by Japanese periodical Forma to present a series of my discoveries. Forma is an official periodical of the Society for Science. The entire issue was devoted to the golden ration and our latest knowledge about it. At the beginning of the article which preceded the presentation I wrote:
“Because I am an artist with philosophical and mathematical interests, my research regarding the golden ration obviously must have differed from the activities undertaken by mathematicians. At first, the main cause of my interest in the golden ratio was its astonishing and surprisingly frequent appearance in art, nature and mathematics. I subconsciously felt that something of such power and uniqueness must have a deeper foundation. In 2000, I discovered the previously unknown world of geometric associations existing in a square and a circle. It was the first visual structure in the world connecting the golden and the silver ratios in one drawing. The discovery started my long journey through the unknown area of beauty, mathematics and philosophy. But it was philosophy that was the main drive and goal of my search. For me geometry is only a visual language for understanding what we see by observing nature; it helps us gain a more comprehensive understanding of the universe so that we could see all the relationships as if in a blink of an eye.
We could say that the source of power in the golden ratio stems from two areas or divisions: firstly, geometry, through the division of a line in accordance with the golden ratio in the same way as discovered in ancient Greece. It is believed that it was already known to Pythagoras but it was Euclid who first described it in Elements in the 4th century BC; secondly, a number as a ratio, discovered by Johannes Kepler (1571–1630) for two subsequent elements of the Fibonacci sequence (1170–1250). I have created the third visual approach in which the golden number is perceived as elements of a greater system of relationships – geometry and number are weaved together in one structure of the universe”.
In the cited fragment from Forma I wish to explain one thing. It involves the immodest act of sharing the credit for the achievements of Pythagoras-Euclid and Fibonacci-Kepler. I wish to take this unique opportunity of the article being featured in a major mathematical periodical to state with full awareness that my discovery is the third in the history of the golden ratio which introduces a dramatically new and surprising element into this most important of proportions. In mathematics there are only three ways of assessing someone’s new proposal: the first – statement that an author made a mistake – this requires proving the error in thought or calculations; the second – statement that an author committed plagiarism – this requires a presentation of an earlier solution; the third – which involves finding neither an error nor fraud – but recognition that we are dealing with something new and that everyone has to admit that as a fact. Mathematicians accept the achievements of people outside their trade – you cannot dispute a person who formulated a theorem and proved it – but they do it only when they have no other choice and it surely does not come easy to them. During conferences, I often felt like an intruder whose innovative association with mathematics seemed to cause them harm. Their secondary easy way of depreciation involves derogation of the importance of a discovery. The more surprising it is to them, the more they pretend that nothing has happened. I knew of this, I experienced it before, therefore I was very meticulous in making sure that my discovery is articulated in that way. Such formulation of the sentence, which eventually proved in print, confirmed in black and white that it was neither a plagiarism and especially that I made no mistake.
The list of names of golden ratio’s researcher is breath-taking: Pythagoras, Phidias, Plato, Euclid, Vitruvius, Fibonacci, Piero della Francesca, Leonardo da Vinci, Johannes Kepler, le Corbusier, Roger Penrose. And others. Many others.
I have discovered a new, unknown and most importantly fundamental rules of the golden ratio. In consequence, the discoveries prove a much more complex nature of the cosmic being of the number. It sounds like a statement of Pythagoras, who said that number is the nature of all things and regarded it as the most important observation.
With this new perspective I understand why the golden ratio was and continues to be somewhat overlooked, marginalised notion. Some believe that it is an odd phantasmagoria – even smart people of the past. They were wrong about many things so would they not be wrong about the assessment of an irrational number which is difficult to remember. I experienced it myself when it happened once more. I knew little outside of the fact that this proportion exists. I did not remember even its estimated value. Can you live without that? You can. But only for some time. The number itself shall ensure that its place in the cosmos is respected.
One time in New York, after a few drinks my artist colleague felt more courageous and asked me what this new thing that I discovered in geometry was. I asked him for paper and drew the first rule which opened the door for me to find further exceptional things. He could not believe it. He said, ‘how is it possible for something so fundamentally simple to be overlooked by everyone?’.
Before I show this first drawing, I am going to write a few words about the historical significance of the golden ratio.
FIRST DISCOVERY
What is proportion? Proportion is the equivalence of ratios. What is ratio? Ratio is – here I shall use the introduction to the topic of the golden proportion by Robert Lawlor in his book Sacred geometry, Philosophy and practice; Thames & Hudson, 2003 – a comparison of two different quantities, amounts, qualities or ideas and it is expressed by a formula A : B (A to B). It can also be written as a fraction A/B. (rys. 1).

rys. 1
The ratio therefore constitutes a measure of the difference, to which at least one of our senses can react. We differentiate a red cup from a green tablecloth only because our optic nerves are capable of telling the difference in frequencies emanating from the cup and the tablecloth. As said by Gregory Bateson, “differences which make the difference”. The solemnity which expresses the name ‘ratio’ is noticeable in Latin and English. The word ‘ratio’ is derived from Latin name ‘ratio’ – ‘reason’ (similarly to the word ‘rational’).
If the ratio is a direct response to a simple difference – the proportion is far more subtle and complex. It comprises four elements: one element is to the second as the third is to the fourth. We write it as: A is to B as C is to D, or A : B : : C : D, or A/B = C/D.
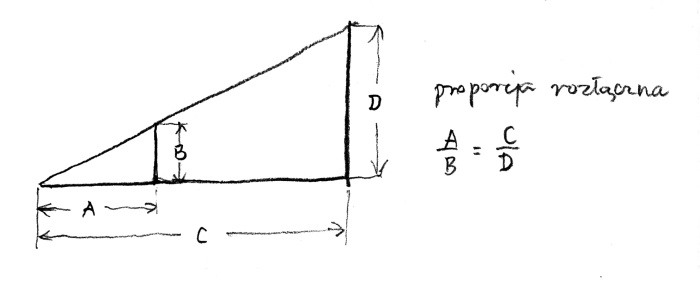
rys. 2
What we need to add here is that in a written proportion the elements A and D are called extremes, whereas B and C are called means. This is important because the products of extreme and mean terms are equal: A x D = B x C. Pythagoreans called this a procedure of thought – non-continuous, disjointed proportion of four elements.
Since this is how they called, it is not difficult to predict that there must exist a continuous proportion comprising three elements. How is this possible when, as said before, a proportion always comprises four elements? It is simple: one element is to the third as the second is to the third. In writing: B is to A as A is to B or B : A : : A : C, or B/A = A/C (rys. 3).
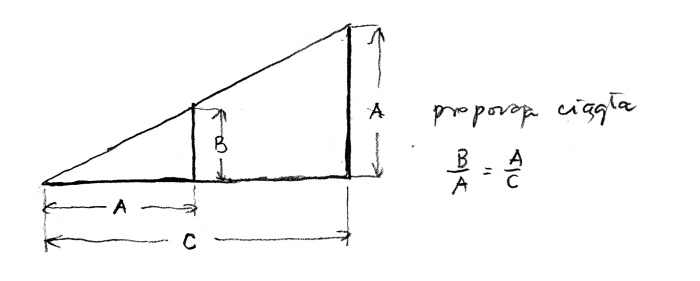
rys. 3
This repetition of the mean element is crucial. Now if we multiply the extreme and mean elements, namely B x C and A x A we get that B x C is equal to A² (A squared). Our proportion becomes not only linear but geometric. This constant proportion of three elements was known as analogy in Greek studies. Analogy has been one of the most important tools in science, law and theology, and in theology it is the most important. It allows it to express the fourth element which, although invisible, remains in a relationship to the others and is their organic consequence, for instant the man is to God-man as God man is to God.
Is it possible to have a proportion comprising two elements? Indeed. The world is full of miracles, and we people sometimes discover them. There is only one and only one proportional division that is possible with the use of only two elements! One element is to the other as the other is to the sum of them. It is written in the form: B is to A as A is to the sum (A and B), or B : A : : A : (A+ B), or B/A = A/(A+B) (rys. 4).
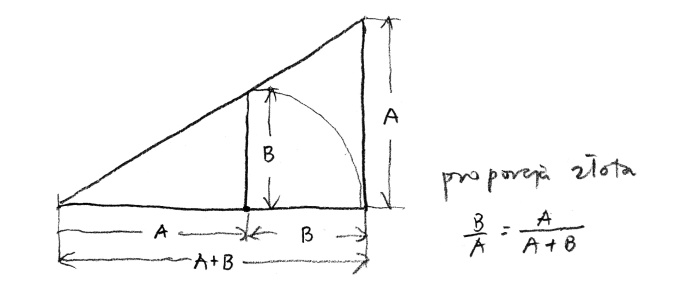
rys. 4
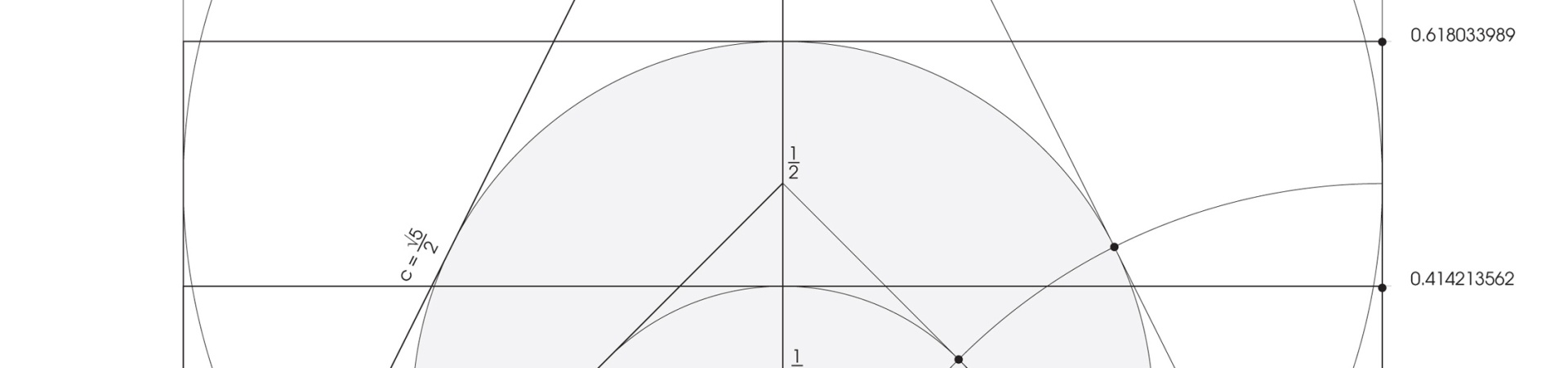
This unique geometric proportion of two elements was given the name Golden Ratio and it is symbolised by the twenty-first letter of the Greek alphabet, Φ (phi). Its numerical value is (√5 +1) / 2 (the square root of 5 plus 1 divided by 2) and is approximately 1.618. The reciprocal is (√5 - 1) / 2 and is equal to 0.618.
Golden ratio (see figure) is a division of a line segment into two parts, longer (A) and shorter (B), so that the shorter part (B) is to the longer (A) as the longer (A) is to the whole section (A + B). The names ‘golden section’, ‘golden ratio’ were introduced only in the 19th century (A Mathematical History of the Golden Number, Roger Herz-Fischler, Dover Publications, Inc., 1998). When Johannes Kepler said his famous sentence about the golden section he of course was referring to as ‘mean and extreme ratio’. He said: “Geometry holds two precious treasures: one of them is the Pythagoras Theorem, the other – a division of a section in mean and extreme ratio. The first can be compared to a measure of gold, the other can be called an invaluable gem”. In order to understand why Luca Pacioli in his book from the 16th century, which was illustrated by Leonardo da Vinci, called the golden ratio not just an invaluable gem but a ‘divine proportion’ (the book was titled De divina proportione), therefore we should go one step, a divine one, further ahead.
Is it possible to formulate a golden ratio formula which uses only a single element? The book De divina proportione, which Pacioli dedicated to Ludovico Sforza, contained five reasons to call it divine. The first and foremost reason was because ‘there is only one God’. Pacioli compares the uniqueness of the golden ratio to the fact that unity ‘is the highest description of God himself’. In order to uncover the mystery of the golden ratio we need to slightly modify the previous drawing (rys. 5).
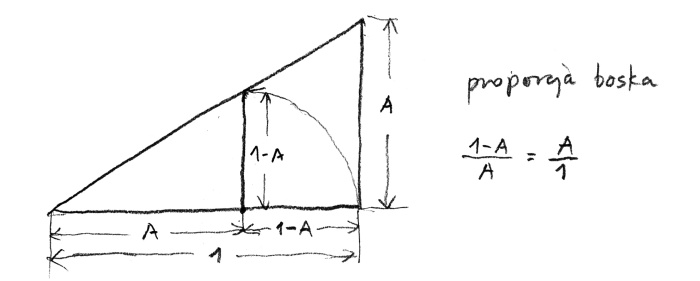
rys. 5
Let us assume that the section we wish to divide has the value of one. When the longer part is described by A, the shorter can be described as 1 - A (one minus A). Acting in accordance with the previously assumed rules we can write: (1 - A) is to A, as A is to 1, or (1 - A) : A : A : 1, or (1 - A)/A = A/1. If we – as we have previously done – multiply the extreme and mean elements we obtain the following equation: (1 - A) x 1 = A x A. There is only a single element there! Is this not divine?
SECOND DISCOVERY
Johannes Kepler had reasons to have a special affection to the golden number. He discovered an unknown way to obtain it and it did not lead through geometry. The genesis of the event took place four centuries earlier. In 1202, Leonardo Fibonacci – an Italian mathematician – wrote a book titled Liber Abaci, in which he provided a convincing proof of the advantage of Hindu-Arabic numerals over Roman numerals. In a certain fragment of the book he told a riddle involving multiplication of rabbits. In the beginning there is a single pair – a male and a female. After a month the pair is of adult age and can spawn another pair. Therefore, on the third month the scene is occupied by two pairs: the parents and the children. According to the rules a pair of children takes a month to mature and the parents can give birth to another pair. The question of Figonacci was: how many pairs of rabbits would there be after 12 months. In the history of mathematics the answer to this simple riddle is very important. It led to the creation of a sequence which since the 19th century is known as Fibonacci sequence. It starts with two ones and two last numbers are always added to form a new number. In the beginning the ‘last numbers’ are only ones. 1 plus 1 equals 2; 2 plus 1 equals 3; 3 plus 2 equals 5. And then in sequence: 8, 13, 21, 34, 55, 89. 144 is the twelfth number of the sequence and that is the answer to Fibonacci’s riddle. The uniqueness of Kepler involved the division of the second last element of the sequence, namely the ‘89’ by ‘144’ and he obtained the number 0.618 – the approximate value of the golden number. This was sensational. The longer the sequence the closer the value of two subsequent numbers is to the golden number. So not only a geometric section but also a sequence are headed towards the same place! This could not have been an accident. The 19th century treated Kepler’s discovery with due seriousness. The numbers of the Fibonacci’s sequence started to appear everywhere: in physical, biological, astronomical and artistic phenomena, even in finances.
This is not the time and place to uncover the riches provided by these two methods of reaching the golden ratio, whether geometrically or mathematically. Very extensive literature is available for that purpose, both paper and digital.
THIRD DISCOVERY
At the foundation of my discovery of the golden proportion there are two observations: one of philosophical nature, and the other – of aesthetic. Let us start with the aesthetic. Every introduction to the golden cut mentions that it is a division of a section into two parts so that the ratio of the shorter part to the longer part is the same to the ratio of the longer part to the whole section. I did not like how the ratio is always depicted in a diagram as travel around the divided section (rys. 6a).
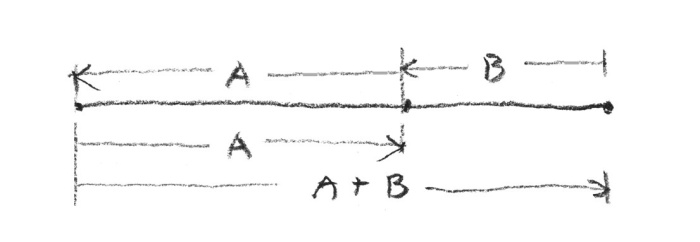
rys. 6a
It revealed the proportion but not the continuity. It seemed to me that it would be more adequate and smart to use the diameter of a circle, which is equal to two radii. It only took for one of them to be divided in the golden ratio for the proportion to stop being static and to suddenly reveal its infinite growth capability: from greatness to smallness (rys. 6b).
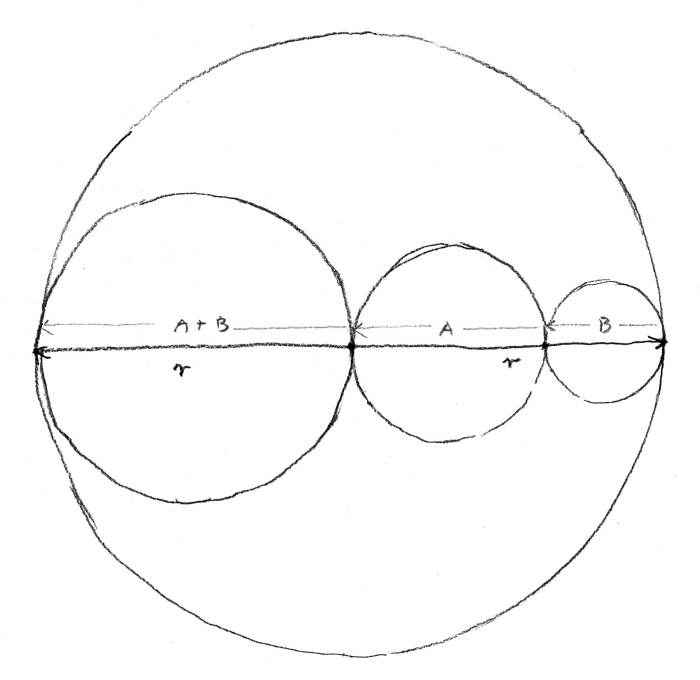
rys. 6b
The second observation is more fundamental. To some degree I had known it from the aforementioned book of Robert Lawlor, Sacred Geometry and from a book titled God’s Secret Formula by Peter Plichta. Contrary to the known Cartesian coordinate system, in which on two sides of an axis passing through the zero point there are placed sequences of positive and negative numbers, Lawlor presented an Egyptian number sequence which began with one. On the right side there was an infinite sequence of natural numbers, while on the left, starting from one – fractions which are the multiplicative inverses of the integers on the right. I realised that if we draw this rule on a number line starting from zero and plot integers and their multiplicative inverses on it, then regardless of how great a number and how far from one we assume, it will be placed between one and zero; for one million it will be one millionth – very close to zero but still within the range one-zero.
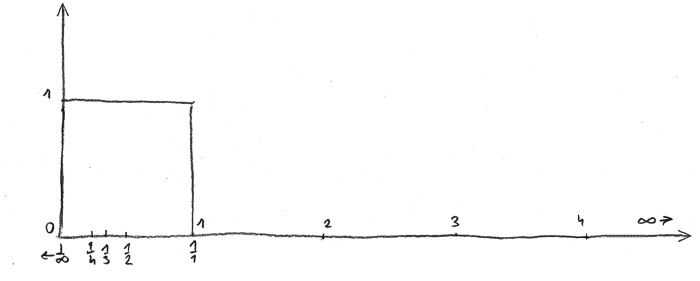
rys. 7
I have drawn a square. If we placed it along the plane of the infinite universe, then through multiplicative inverses each point of that universe will fit inside a drawn square, just as images fit in a human eye. This was shocking to me. Just like Borges I have found my aleph point.
What did I draw for my artist friend in New York? At first, I have drawn a square. (rys. 8).
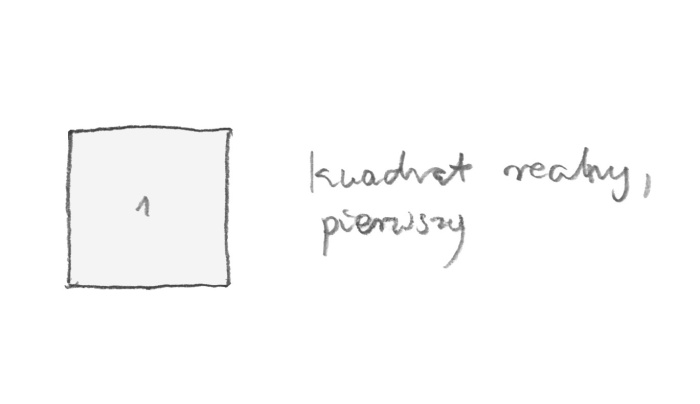
rys. 8
A square is important. It is a genesis of reality. When something exists, it is one. All squares start from one. Without one, not only there is no square but there is nothing. In Pythagoras’s memory I took ten squares. (rys. 9).
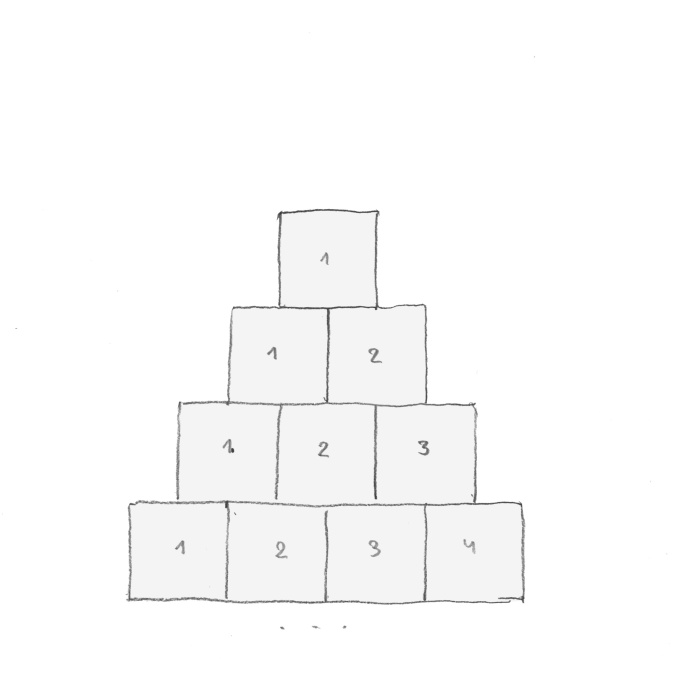
rys. 9
For him, ten (1 + 2 + 3 + 4 = 10) was a holy and perfect number. I assembled a pyramid (tetractys) but not from points as Pythagoreans did it, but by using squares
I have plotted lines which are tangent to the squares. (rys. 10).
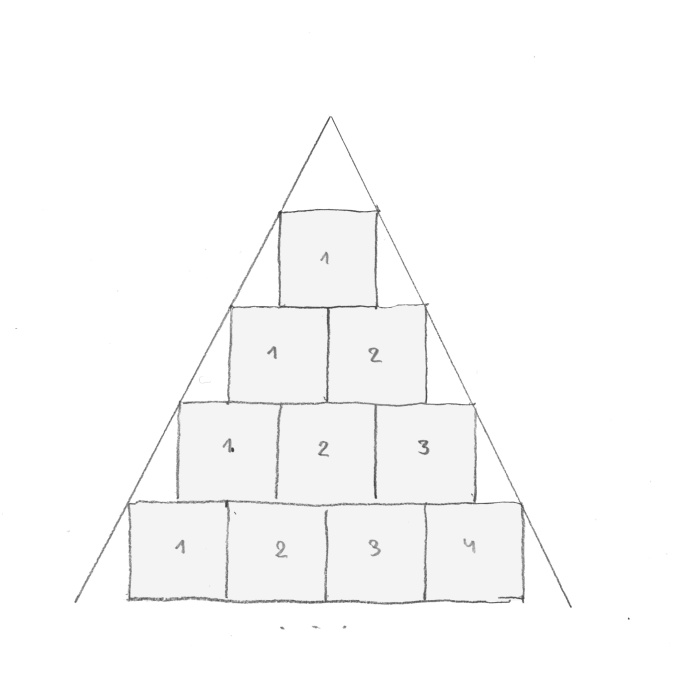
rys. 10
The tangent lines meet in an empty space above square one. As I mentioned before, everything in real world begins with one. Where do those tangent lines meet? I named the first square ‘real’ while the non-existing square above it I called ‘virtual’, ‘spiritual’ (rys. 11).
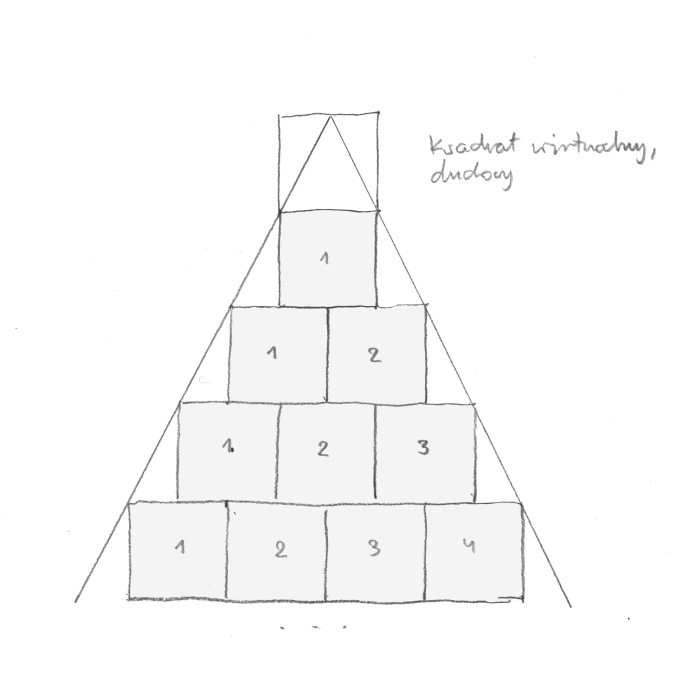
rys. 11
In the next step I have inscribed circles in the squares and plotted tangent lines alongside them (rys. 12).
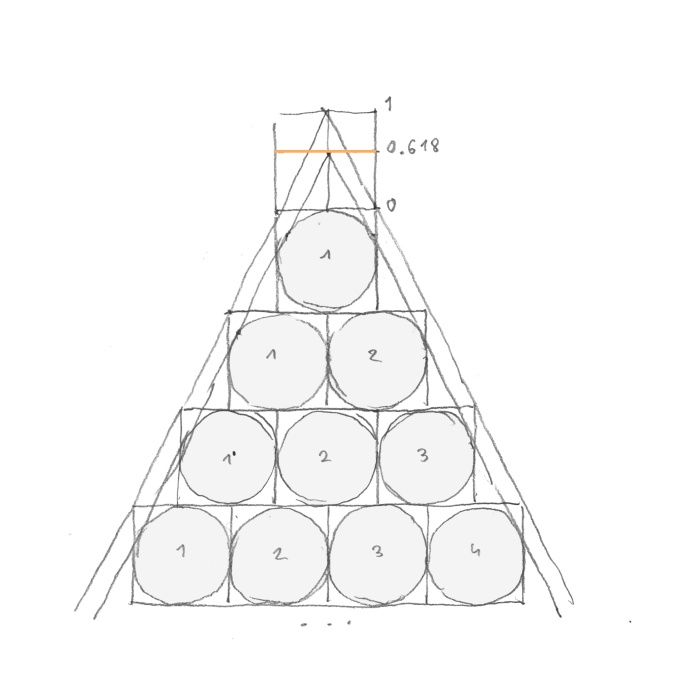
rys. 12
That was the moment when a miracle occurred. As it turns out the lines tangent to the circles are displaced in relation to the lines tangent to the squares in golden ratio! Square and circle are the two most important shapes in the universe. ‘How is it possible for something so fundamentally simple to be overlooked by everyone?’ – as you remember – was what my friend said.
Nobody has ever noticed their divine connection.
I have concentrated on the newly created virtual-spiritual square. Even though it does not exist, yet such crucial events are being uncovered inside it (rys. 13).
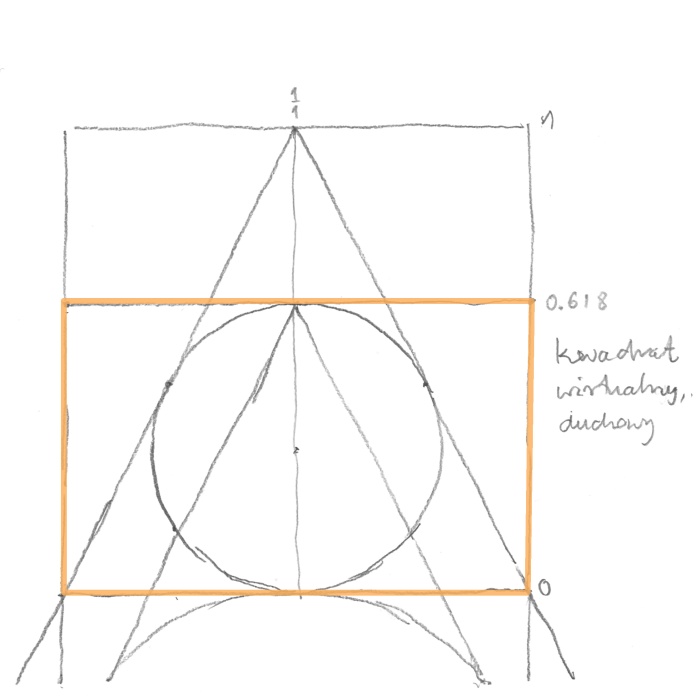
rys. 13
If through the point where the lines tangent to the circles meet we plot a line in parallel to the base of the virtual square, it will create a golden rectangle. When I inscribed a circle inside the golden rectangle, I was surprised to see that it touches the square tangents from which everything had begun. This golden circle is inscribed in a triangle with a base of one and a height of one. By reversing the observation I could express a surprising theorem – a diameter of a circle inscribed in a triangle with a base of one and a height of one creates a golden ratio with the base (and height) of that triangle. Nobody has ever noticed it.
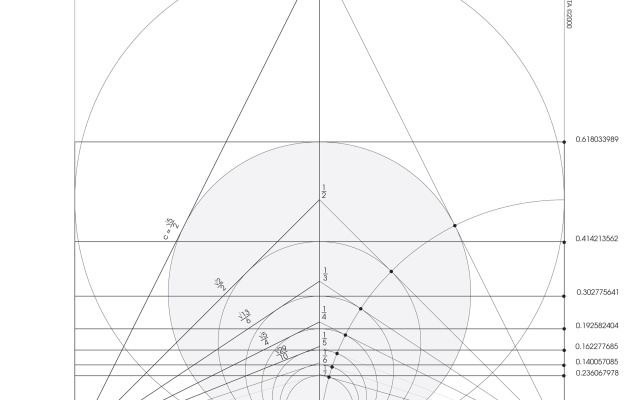
I learned from Jay Kappraff that apart from the golden ratio there is another type of division, called silver ratio, based on the same principle (actually it should be said that there is an infinite number of silver divisions, the first of which we call golden ratio).
Their deep connection is visible in particular clarity in a continued fraction. We shall not focus too much on the fraction itself but let us behold its beautiful and visual power. When we describe the silver number with ‘Sn’, and the sequential number with ‘n’, then the general continued fraction for all silver divisions will look like the example below.
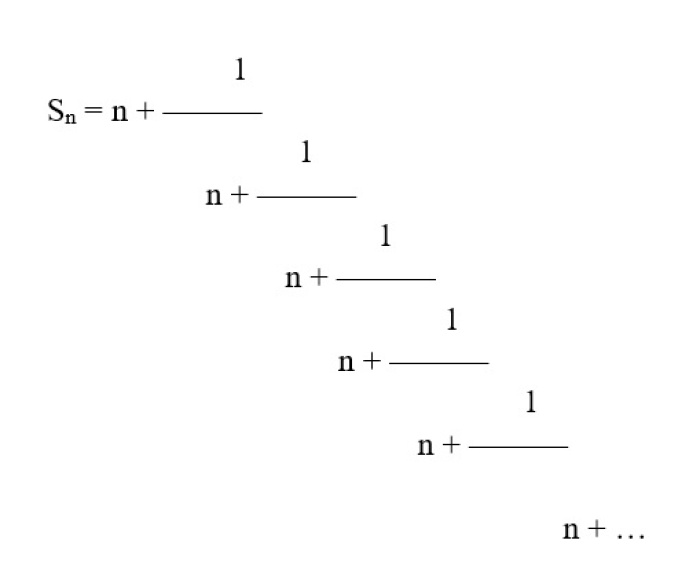
Now when we substitute number 1 we obtain 1.618, the golden ratio, as the first number.
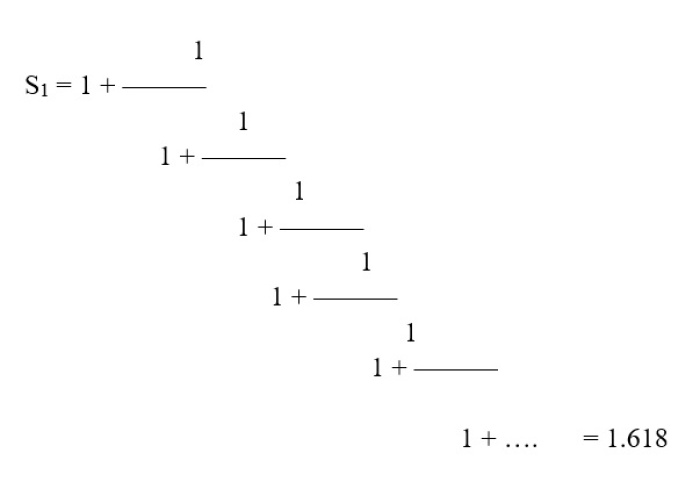
For n = 2 we obtain another silver number, 2.4142
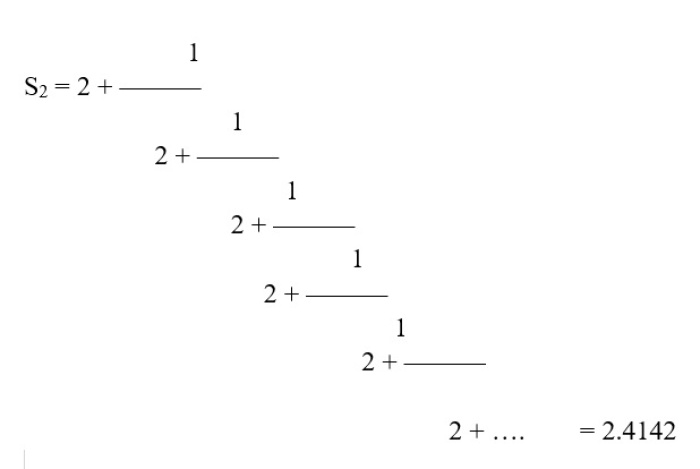
Of course by substituting subsequent integers we can produce an infinite number of silver numbers. What is shocking about the continuous fraction, especially one representing the golden ratio, is that it is made of only number one. Unity in relation with itself leads infinitely towards the golden number! Shocking.
Another visual way of presenting the rule of silver division is their association with squares. If from one of the first divisions in a sequence – the golden rectangle – we cut off a square, the cut part we cut off is once again a golden rectangle (rys. 14).
rys. 14
In the second silver rectangle we have to cut off two squares in order to obtain a smaller silver rectangle. And so forth. Just as a reminder – the façade of the Acropolis is in golden ratio, and the façade of Vatican – in silver ratio.
Once aware of the existence of the silver ratios after the meeting with professor Kappraff I returned home, I was eager to test a certain odd suspicion. As you remember when you inscribe a circle in a triangle with a base of one and a height of one it becomes a golden circle. What will happen, which is what was suspicious to me, if we inscribe a circle in a triangle with a base of one and a height of 1/2 (one-half)? Yes. This was my eureka – a circle inscribed in a triangle plotted a silver ratio! (rys. 15)
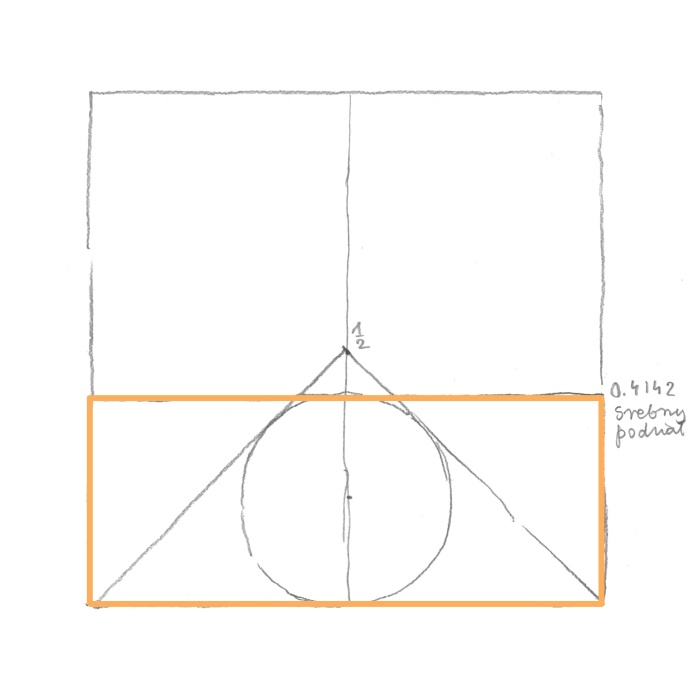
rys. 15
Until that moment in order to draw a golden ratio and a silver ratio it was necessary to use of two different drawings. For the first time in history I was able to create a schematic/structure/mechanism which would tie them together and depict previously unknown relationships (rys. 16).
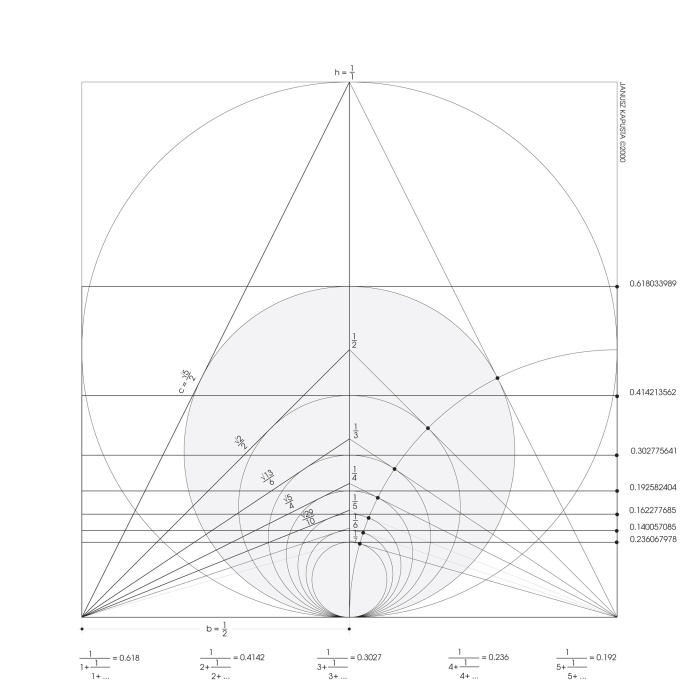
rys. 16
It was at that moment when prof. Jay Kappraff invited me to write an article for Forma. Then the next discoveries followed. They convinced me that not only was I not wrong but I started to connect the previously separate occurrences in one sequence.
THIRD DISCOVERY – CONCLUSIONS
My discoveries have shown that the golden ratio is unique and complex and that when it is viewed as the FIRST in the infinite sequence of proportions, it manifests itself as a fundamental relationship in the structure of the universe. The golden ratio is no longer an isolated island of beauty. Because it is the FIRST and because of its intimate connection to number One, the golden centre leaves an important mark on the behaviour of cosmos.
The golden division – like a sperm cell which although the competition among millions in a race for the egg cell has won, it was the first – it also leaves its mark on everything. On the world, cosmos, nature and also on the thoughts and feelings of people. People are very different and yet all of us are human, each has the same code, algorithm, number. We do not need to learn gravity. Same goes for the golden ratio. They live within us.
In order to convince – myself in the first place – that there is sense in it, I started to explore basic primitive peasant cultures. I was aware that they knew nothing about the golden ratio. At least not consciously. What about subconsciousness?
If, as the structure suggested, the golden ratio is a matrix, an archetype in a Jungian sense (archetypes – structural elements of the collective unconscious, common to all people in the world), they had to reflect the golden ratio. Yes – peoples of America, Africa, Asia and Europe without knowing about the golden ratio they have always revealed it in its acts associated with beauty. If you do not believe it, see for yourselves. To conclude, I wish to present only one example. I will use a painter from Poland. He knew nothing about the golden ratio. His name was Nikifor (rys. 17)

rys. 17
In a courthouse during very complicated cases an enormous amount of documentation is being produced. Tens, hundreds, thousands of pages. All for the purpose of allowing the judge/reader to – based on the evidence – say but one word: guilty or innocent. I do not know whether this relatively short text is capable of allowing the reader to reach a guilty-innocent decision. I only wish to ensure that the documentation inside the book I am preparing will be far more comprehensive, in-depth and astounding. But not different.
Its conclusion will state that Beauty is not just a notion made-up by some intellectuals and artists, but a foundation of the universe. Just like Good and Truth.
Beauty is the only face of God which could not be hidden away
Janusz Kapusta, Plus Minus, [in:] Podręcznik do myślenia, Zysk i S-ka, 2014
Drawing: Ignacy Czwartos